Decomposed and coordinated operation of multi-area system

The multi-area system decomposed and coordinated operation (DCO) is studied to make better utilization of large-scale inter-connected power systems to optimize resource utilization in a wider geography. In the DCO scheme, the global optimization is achieved by the information interaction between the coordinator and intra-regional system operators. In this area, a novel decomposition coordination approach based on dynamic multipliers is proposed. By utilizing a sensitivity analysis method, the Lagrangian multipliers of sub-problems are extended from constants to dynamic functions of coupled variables, which enables the sub-problems to predict the change of multipliers and, therefore, facilitates the convergence of decentralized optimization. The proposed approach can significantly improve the computational efficiency of decomposition and coordination. The proposed decomposition coordination algorithm is employed to solve the multi-area DC-OPF, which is the basic model of the day-ahead generation scheduling. The proposed decomposition coordination algorithm is also capable of solving the multi-area AC-OPF to realize the intra-day generation scheduling.

Iterative evolution of tie-line flows computed by the two adjacent area. (a) via static multiplier method. (b) via the proposed dynamic multiplier method.

References

• Lai X , Xia Q , Xie L . Inter-area power exchange preserving multi-area economic dispatchC Pes General Meeting | Conference & Exposition. IEEE, 2014.

• Lai X , Zhong H , Xia Q , et al. Decentralized Intraday Generation Scheduling for Multiarea Power Systems via Dynamic Multiplier-Based Lagrangian RelaxationJ. IEEE Transactions on Power Systems, 2016:1-10.

Inducting objective function algorithm for large-scale MILP

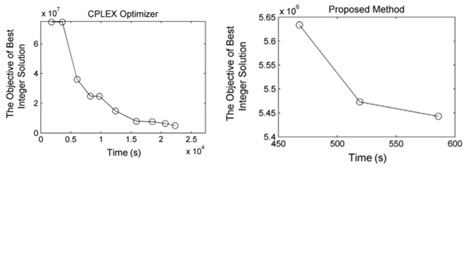
An efficient method to solve the long-term security constrained unit commitment (SCUC) is a requisite for power system operators in many countries, particularly those with many coal-fired generating units, which require a long time to start up and shut down. However, the complexity that is introduced by the energy or fuel constraints in the long-term SCUC problem often results in exorbitant computation time. Motivated by this, a new type of approach, which is termed the inducing-objective-function (IOF)-based method, is proposed. This method significantly improves the computational efficiency. In the proposed method, the inducing factors are introduced into the objective function of the SCUC relaxation problem to induce more UC state variables to satisfy the integrality requirement after several iterations. According to the relaxation solution, the objective function of the original SCUC model is modified. Thus, the process of solving the modified model using the branch-and-cut algorithm can be more efficient. Because the solution of this modified model can be near-optimal for the original model, the gap between the near-optimal and the optimal solution is estimated to decide whether the near-optimal solution is acceptable for practical application. If the near-optimal solution is not acceptable, it will be used as the initial solution to solve the original model. Because the initial solution is of high quality, it can significantly speed up the branch-and-cut process.

Comparison of computational efficiency between the CPLEX MILP solver and the proposed method.

References

• Yang B, Zhong H, Xia Q, et al. Inducing-objective-function-based method for long-term SCUC with energy constraintsJ. International Journal of Electrical Power & Energy Systems, 2014, 63(4):971-978.

• Wang Y , Zhong H , Xia Q , et al. An Approach for Integrated Generation and Transmission Maintenance Scheduling Considering N-1 ContingenciesJ. IEEE Transactions on Power Systems, 2015.

Network aggregation theory and method for inter-regional and multi-level system coordination

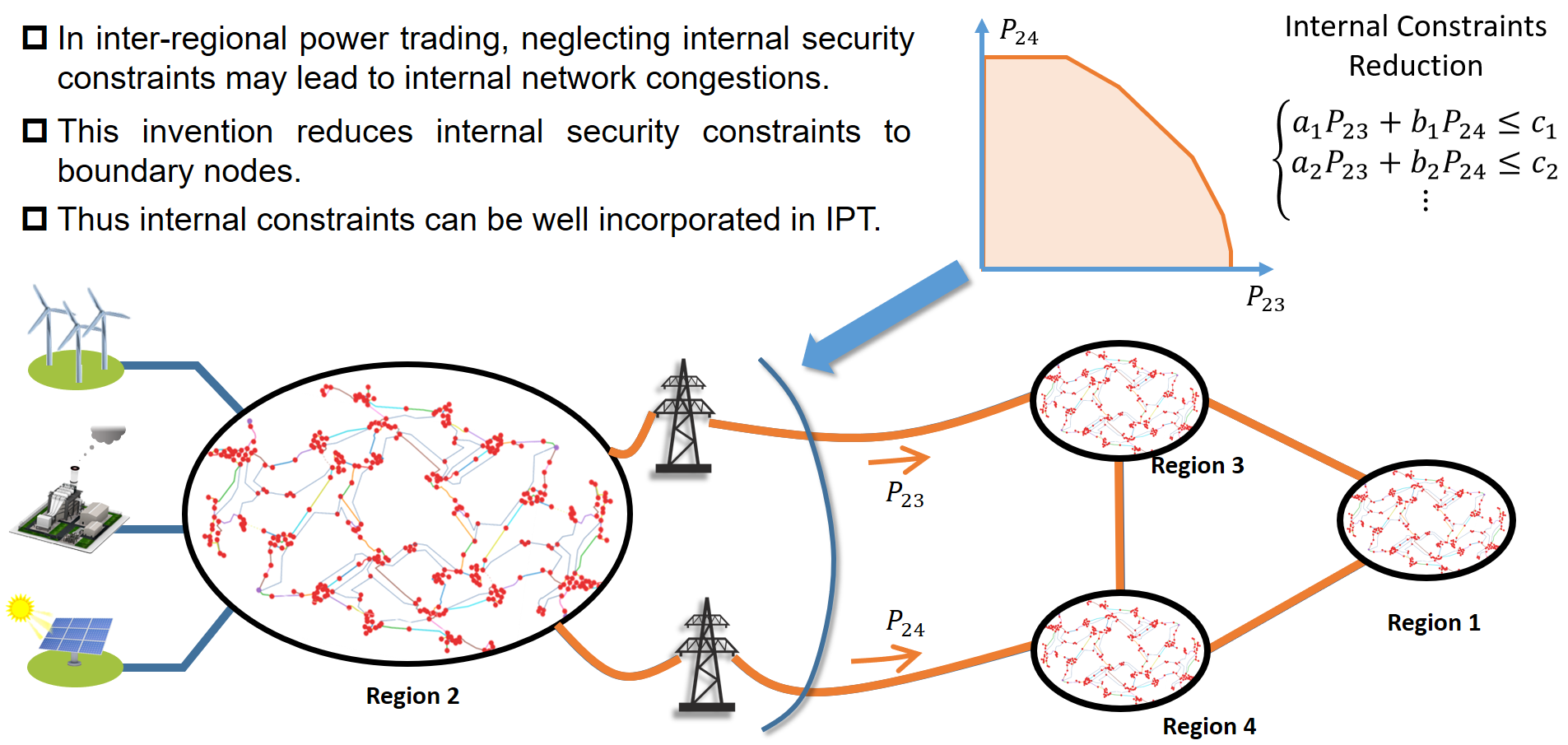
Conventional network reduction and aggregation methodologies, e.g., the Norton equivalence, only concern the boundary equivalence of the network equations. The internal system operating constraints, however, are ignored. To facilitate the inter-regional power trading and the coordination between the transmission system and the distribution systems, it is beneficial for the coordinator and the upper-level system operator to know the aggregated operating feasible region of the subsystems. This motivates us to extend the conventional network reduction methodologies to incorporate the internal system operating constraints when studying the external equivalent characteristics of a system. The innovated methodology is based on the projection theory. We partition the variables into two types, namely the internal state variables and the boundary coordination variables. By project the feasible region with regard to the internal state variables onto the subspace of the coordination variables, the external equivalence incorporating both the network equation and the operating constraints can be evaluated. We also propose a novel polyhedron projection algorithm which calculate the projection by enumerating vertices of the projected polytope in a breath-first manner. The computation efficiency of the proposed algorithm outperforms the classical Fourier elimination algorithm by 5 8 times. The proposed algorithm can also tackle large-scale network problems. The proposed network aggregation theory and algorithm is studied to realize the non-iterative inter-regional market clearing and the TSO-DSO coordination.

The inter-regional market clearing scheme based on the proposed network aggregation theory.

References

• Zhenfei Tan, Haiwang Zhong, Jianxiao Wang, Qing Xia, Chongqing Kang. Enforcing Intra-regional Constraints in Tie-line Scheduling: A Projection-Based Framework J. IEEE Transactions on Power Systems, 2019.

• Zhenfei Tan, Haiwang Zhong, Qing Xia, Chongqing Kang, et al. Estimating the Robust P-Q Capability of a Virtual Power Plant under Uncertainties J. IEEE Transactions on Power Systems, (under review).

• Zhenfei Tan, Haiwang Zhong, Qing Xia, Junfeng Yang. Bi-level Electricity Market Design with Boundary Equivalence of Interior Security ConstraintsC European Energy Market. IEEE, 2018:1-5